Blog
Troisième cours : Les systèmes et la réduction (ou élimination)
Cette deuxième méthode est différente de la première :
Prenons le même système :
Prenons le même système :
![Rendered by QuickLaTeX.com \[\begin{cases} $ 2x + 3y = 4 $ \\ $ 3x + 2y = 8 $ \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-43e90469b65699168553583a2dcd9dc2_l3.png)
Pour réduire (ou éliminer) une inconnue d’une des deux équations il faut la supprimer. Pour ce faire, il faut donc tout d’abord que les deux inconnues aient un facteur commun. Pour ce faire, ici, nous allons multiplier l’entièreté de la première équation par le facteur de l’inconnue que nous voulons supprimer de la Seconde équation. L’équation va être multipliée par 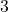 et inversement : la seconde équation va être multipliée par le facteur de l’inconnue de la première équation que nous souhaitons supprimer, soit
et inversement : la seconde équation va être multipliée par le facteur de l’inconnue de la première équation que nous souhaitons supprimer, soit 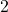 .
Cela donnera ceci (les facteurs communs sont surlignés en rouge) :
.
Cela donnera ceci (les facteurs communs sont surlignés en rouge) :
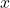 de notre première équation :
de notre première équation :
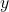 :
:
Comme nous avons trouvé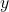 nous allons donc pouvoir résoudre la seconde équation :
nous allons donc pouvoir résoudre la seconde équation :
Ainsi, le système d’équation est défini par le couple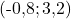 .
.
![Rendered by QuickLaTeX.com \[\begin{cases} $ \redHighlight{3} * (2x + 3y) = \redHighlight{3} * 4 $ \\ $ \redHighlight{2} * (3x + 2y) = \redHighlight{2} * 8 $ \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-3390002662730c1cdf3b2af69781338f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6x + 9y = 12 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-2fda0c3356bebba74079399cc4be27d0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6x + 9y - (6x + 4y) = 12 - 16 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-be1bdf2973cff3f3cd64175a7b68b8af_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6x + 9y - 6x - 4y = \text{-}4 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-ea787e5bc7d8ff8dfe26a3cd9983455f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 9y - 4y = \text{-}4 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-fca3c6b4c4f48e86ff874b30381541ce_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 5y = \text{-}4 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-4a62fb3ca6cefa92dd3a3612266e33dc_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \dfrac{\text{-}4}{5} = \text{-}0{,}8 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-f71c7aa68e4170a83e9e935f988cdc53_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ 6x + 4y = 16 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-73173292146f69da1ef1be431b287348_l3.png)
Comme nous avons trouvé
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ 6x = 16 - 4*(\text{-}0{,}8) \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-feab53ac4034bc85eb8cc955a460572a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ 6x = 16 + 3{,}2) \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-07a434c13d2753dd50842da661c532ce_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ 6x = 19{,}2) \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-3b8ab408253a411e135adf31fbd105f2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ x = \dfrac{19{,}2)}{6} \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-56c0c9dcb065d2137124591e18fbb56c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y = \text{-}0{,}8 \\ x = 3{,}2 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-a558fb3e505f6628c5f7df43d5a89aca_l3.png)
Ainsi, le système d’équation est défini par le couple
Autour de ces deux notions et au travers des deux derniers cours j’ai fait faire à Élias environ 3 à 4 exercices afin de m’assurer qu’il avait bien compris cette notion.
Ci-dessous une photo d’un exercice qu’Élias a fait durant le dernier cours.
Ci-dessous une photo d’un exercice qu’Élias a fait durant le dernier cours.