Blog
Troisième cours : Les systèmes et la substitution
Ce mardi 13 février 2024 je vais donner mon troisième cours de mathématiques à Elias : cela va porter sur les systèmes d’équations.
Pour commencer le cours, je lui ai expliqué et défini ce qu’était un système et je le lui ai démontré par deux démonstrations différentes que je vais présenter. Un système d’équations est un ensemble d’équations, utilisant les mêmes variables ou inconnues ; une solution est l’affectation d’une valeur à chacune de ces variables, de telle façon que toutes les équations du système soient satisfaites simultanément.
De fait, voici ci-dessous la première démonstration d’une résolution d’un système d’équation :
Pour commencer le cours, je lui ai expliqué et défini ce qu’était un système et je le lui ai démontré par deux démonstrations différentes que je vais présenter. Un système d’équations est un ensemble d’équations, utilisant les mêmes variables ou inconnues ; une solution est l’affectation d’une valeur à chacune de ces variables, de telle façon que toutes les équations du système soient satisfaites simultanément.
De fait, voici ci-dessous la première démonstration d’une résolution d’un système d’équation :
Prenons le système :
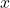 en fonction de
en fonction de 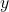 dans la première équation système :
dans la première équation système :
d’où
c’est à dire
Puis nous allons remplacer x dans la seconde équation du système par ce qui a été trouvé plus haut dans la première équation :
En développant, nous allons obtenir :
Puis il va maintenant falloir résoudre la seconde équation :
c’est à dire :
d’où
Une fois que nous avons trouvé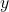 , il faut maintenant le remplacer dans la première équation afin de trouver
, il faut maintenant le remplacer dans la première équation afin de trouver 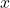 :
:
soit :
Ainsi, le système d’équation est défini par le couple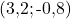
![Rendered by QuickLaTeX.com \[\begin{cases} $ 2x + 3y = 4 $ \\ $ 3x + 2y = 8 $ \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-43e90469b65699168553583a2dcd9dc2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 2x = 4 - 3y \\ 3x + 2y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-e2fbda5f41db51f981a705f887230a81_l3.png)
d’où
![Rendered by QuickLaTeX.com \[\begin{cases} x = \dfrac{4 - 3y}{2} \\ 3x + 2y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-1b069fb0057f3054b86ed31c57e1a732_l3.png)
c’est à dire
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ 3x + 2y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-d2bf26d9b5dbfb2416ebfece926958be_l3.png)
Puis nous allons remplacer x dans la seconde équation du système par ce qui a été trouvé plus haut dans la première équation :
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ 3*(2 - 1{,}5y) + 2y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-82dd0da78fc11e97ff653a5a4f699fcf_l3.png)
En développant, nous allons obtenir :
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ 6 - 4{,}5y) + 2y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-dbc84dc99b5a015f08b35d842c0d0422_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ 6 - 2{,}5y = 8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-1e18c04e14b4938a272a5e3143ccc415_l3.png)
Puis il va maintenant falloir résoudre la seconde équation :
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ \text{-}2{,}5y = 8 - 6 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-904798b99343c702eef9ca43c3f3958d_l3.png)
c’est à dire :
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ \text{-}2{,}5y = 2 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-de44b834f65f26718a539ba297b4da3c_l3.png)
d’où
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5y \\ y = \dfrac{2}{\text{-}2{,}5} = \dfrac{\text{-}2}{2{,}5} = \text{-}0{,}8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-0db4eaae8b1c868f57c041c4b631405b_l3.png)
Une fois que nous avons trouvé
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}5*(\text{-}0{,}8) \\ y = \text{-}0{,}8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-9406cc06c51959114b60bc503fb141e8_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x = 2 - 1{,}2 = 3{,}2 \\ y = \text{-}0{,}8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-6fdd5937741d5fd435a7ad7b7f6003fb_l3.png)
soit :
![Rendered by QuickLaTeX.com \[\begin{cases} x = 3{,}2 \\ y = \text{-}0{,}8 \end{cases}\]](https://pierre-ange.delbary-rouille.net/wp-content/ql-cache/quicklatex.com-8f2133aab2905b46e71976ee33d858b6_l3.png)
Ainsi, le système d’équation est défini par le couple
