Blog
Premier cours : Exercices
Après avoir reformulé le contenu du cours sur la relation de Chasles et le calcul de la norme d’un vecteur avec Elias, je lui ai fait faire de petits exercices portant sur ces notions.
Nous avons commencé premièrement par l’exercice 2 page 184 du manuel de seconde de Mathématique « Le livre scolaire » dont l’énoncé est retranscrit ci-dessous :
Exercice 28:
On considère la figure suivante composée de triangles équilatéraux.

Recopier et compléter les phrases suivantes :
- Le point D a pour image le point … par la translation de vecteur
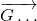
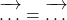 signifie que
signifie que  est l’image de
est l’image de  par la translation de vecteur
par la translation de vecteur 
Corrigé:
Il est indiqué dans cet énoncé qu’il faut compléter les phrases par des points ou des vecteurs.
Élias a répondu aux questions en complétant les phrases :
- Le point D a pour image B par la translation de vecteur GK
- DB=GK signifie que B est l’image du point D par la translation de vecteur GK.
Ce premier exercice a permis à ÉLIas de se familiariser à nouveau avec les vecteurs et il n’y a pas eu de problèmes particulier. Élias l’a réussi avec brio.
Après cet exercice, nous avons continué avec l’exercice 41 page 181 du même manuel avec l’énoncé ci-dessous :
Exercice 41:
On considère la figure suivante constituée de triangles équilatéraux :
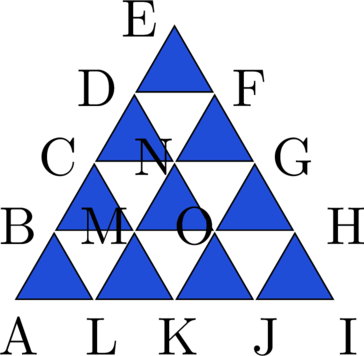
- Ecrire trois égalités traduisant la relation de Chasles.
- Ecrire trois égalités traduisant la propriété du parallélogramme.
- Réduire les sommes suivantes en transformant l’égalité si nécessaire:
Dans cet exercice, Élias a dut mettre en œuvre tout ce qui avait été vu précédemment dans le cours concernant la relation de Chasles. Pour rappel, toutes les réponses retranscrites ci-dessous et dans les exercices à venir sont celle d’Élias et non une correction de l’exercice.
Corrigé:
Question 1. Les trois égalités traduisant la relaiton de Chasles sont :
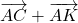
- Selon la propriété du parallélogramme,
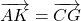
- Donc
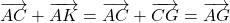
- Selon la propriété du parallélogramme,
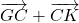
- Selon la relation de Chasles, on peut dire que
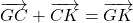
- Selon la relation de Chasles, on peut dire que
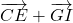
- Pas de réponnse.
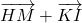
- Selon la propriété du parallélogramme,
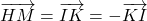
- Donc
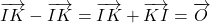
- Selon la propriété du parallélogramme,
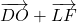
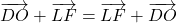
- Selon la propriété du parallélogramme,
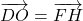
- Donc
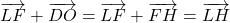
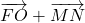
- Selon la propriété du parallélogramme,
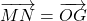
- Donc
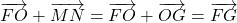
- Selon la propriété du parallélogramme,
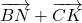
- Selon la propriété du parallélogramme,
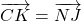
- Donc
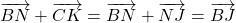
- Selon la propriété du parallélogramme,
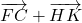
- Pas de réponse.
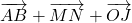
- Selon la propriété du parallélogramme,
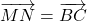 et
et 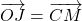
- Donc
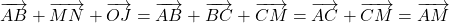
- Selon la propriété du parallélogramme,
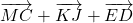
- Pas de réponse.
Les réponses d’Élias étaient toutes justes, sauf 3 questions auxquelles il n’as pas répondu. Je lui ai alors expliqué comment résoudre ces problèmes qui en fait ne sont que de l’application de ce qui a été vu précédemment, mais une application alambiquée, de sorte que 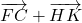 est égal à
est égal à 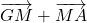 car
car 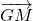 et
et 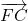 sont parallèles car GMCF forme un parallélogramme de même que
sont parallèles car GMCF forme un parallélogramme de même que 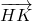 et
et 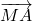 sont similaires car HKAM forme un parallélogramme.
sont similaires car HKAM forme un parallélogramme.
C’est ainsi que s’est terminé mon premier cours avec Élias, cours très intéressant et très instructif pour lui comme pour moi car j’ai pu voir quel étaient ses difficultés sur le sujet, mais aussi ses points forts.
C’est ainsi que s’est terminé mon premier cours avec Élias, cours très intéressant et très instructif pour lui comme pour moi car j’ai pu voir quel étaient ses difficultés sur le sujet, mais aussi ses points forts.
