Blog
Deuxième cours : Exercices
Après avoir fait à Elias la même présentation que celle décrite ci-dessus, je lui ai donné des exercices à faire sur ce sujet :
Le premier exercice concernait le traçage du tableau de variation de différente fonction affines :
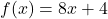 Cette fonction est croissante car le coefficient multiplicateur
Cette fonction est croissante car le coefficient multiplicateur 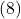 est positif :
est positif :
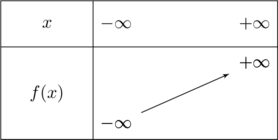
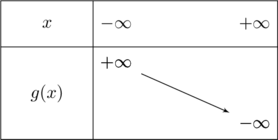

Il s’agissait du premier exercice qu’Elias a fait.
Le second consistait résoudre un problème à partir des fonctions précédentes 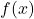 et
et 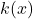 :
Reprendre les fonctions
:
Reprendre les fonctions 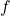 et
et 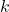 de l’exercice précédent.
de l’exercice précédent.
Pour les questions 2 et 3 j’ai réalisé une légère adaptation de l’énoncé en remplaçant tableau de signe par tableau de variation, deux choses différentes.
Élias à bien réussi pour la fonction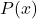 , mais à un peu peiné pour la fonction
, mais à un peu peiné pour la fonction 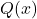 , ce qui est compréhensible de mon point de vue car il s’agissait d’une fonction hyperbolique qui ne passait pas par
, ce qui est compréhensible de mon point de vue car il s’agissait d’une fonction hyperbolique qui ne passait pas par 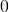 , or, c’est quelque chose de tout nouveau en seconde.
, or, c’est quelque chose de tout nouveau en seconde.
Après ces deux exercices, le cours fut fini, j’ai pu durant cette séance ré-expliquer à Élias les variations de fonctions avec le coefficient directeur et les tableaux de signes. Pour la prochaine séance, nous avons convenu que cela porterait sur les systèmes d’équations.
- Déterminer l’ensemble de définition des fonctions
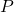 et
et 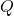 définies respectivements par
définies respectivements par 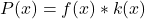 et
et 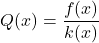 .
. - Dresser le tableau de sines de la fonction
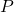 sur son ensemble de définition.
sur son ensemble de définition. - Dresser le tableau de sines de la fonction
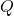 sur son ensemble de définition.
sur son ensemble de définition.
Pour les questions 2 et 3 j’ai réalisé une légère adaptation de l’énoncé en remplaçant tableau de signe par tableau de variation, deux choses différentes.
Élias à bien réussi pour la fonction
Après ces deux exercices, le cours fut fini, j’ai pu durant cette séance ré-expliquer à Élias les variations de fonctions avec le coefficient directeur et les tableaux de signes. Pour la prochaine séance, nous avons convenu que cela porterait sur les systèmes d’équations.
